Быстрое преобразование Фурье⁚ алгоритмы и приложения
Быстрое преобразование Фурье (БПФ) – это алгоритм, который революционизировал обработку сигналов и стал неотъемлемой частью множества современных технологий. Он позволяет значительно ускорить вычисление дискретного преобразования Фурье (ДПФ), что открывает широкие возможности для анализа и обработки данных в самых разных областях, от обработки изображений и звука до телекоммуникаций и биомедицины. В этой статье мы углубимся в мир БПФ, рассмотрев его основные алгоритмы и наиболее впечатляющие приложения. Вы узнаете, как этот мощный инструмент работает и почему он так важен для современного мира.
Дискретное Преобразование Фурье⁚ Основа БПФ
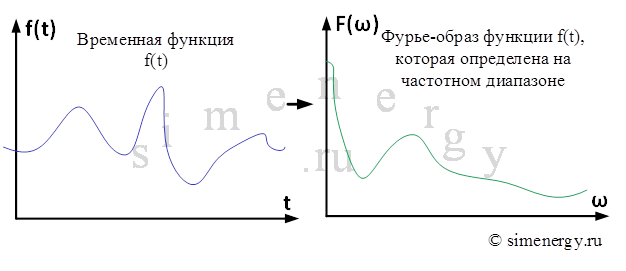
Прежде чем погрузиться в алгоритмы БПФ, необходимо понять, что такое дискретное преобразование Фурье (ДПФ). ДПФ – это математическая операция, которая преобразует последовательность данных во временной области в эквивалентную последовательность в частотной области. Другими словами, оно позволяет разложить сложный сигнал на составляющие его частоты, определив амплитуду и фазу каждой из них. Это крайне полезно, поскольку многие процессы и явления в природе и технике описываются проще в частотной области, чем во временной.
Однако прямое вычисление ДПФ по стандартной формуле требует O(N2) операций, где N – количество точек данных. Это становится крайне ресурсоемким при обработке больших объемов информации. Именно здесь на помощь приходит БПФ.
Алгоритмы Быстрого Преобразования Фурье
БПФ – это не один конкретный алгоритм, а семейство алгоритмов, которые эффективно вычисляют ДПФ за O(N log N) операций. Это огромное преимущество по сравнению с прямым вычислением ДПФ, особенно при больших значениях N. Наиболее распространенным и эффективным алгоритмом БПФ является алгоритм Кули-Тьюки, основанный на принципе "разделяй и властвуй".
Алгоритм Кули-Тьюки рекурсивно разбивает исходную последовательность данных на меньшие подпоследовательности, вычисляет ДПФ для каждой из них и затем объединяет результаты. Этот подход позволяет значительно сократить количество необходимых вычислений. Существуют и другие алгоритмы БПФ, например, алгоритм Радемахера-Вале-Пуссена, каждый со своими преимуществами и недостатками, выбор которых зависит от конкретной задачи и требований к производительности.
Алгоритм Кули-Тьюки⁚ Подробное рассмотрение
Алгоритм Кули-Тьюки работает, рекурсивно деля входной массив на два меньших массива, вычисляя ДПФ для каждого из них, и затем комбинируя результаты с помощью операций сложения и умножения. Этот процесс повторяется до тех пор, пока не будут получены ДПФ для массивов размера один. Эффективность алгоритма обусловлена тем, что многие вычисления повторяются и могут быть повторно использованы. Это приводит к значительному снижению вычислительной сложности.
Приложения Быстрого Преобразования Фурье
БПФ нашло широкое применение в различных областях науки и техники. Его универсальность и эффективность сделали его незаменимым инструментом в обработке сигналов и данных. Рассмотрим некоторые из ключевых областей⁚
| Область | Применение БПФ |
|---|---|
| Обработка изображений | Сжатие изображений (JPEG), фильтрация изображений, распознавание образов |
| Обработка звука | Сжатие звука (MP3), шумоподавление, анализ музыкальных сигналов |
| Телекоммуникации | Модуляция и демодуляция сигналов, кодирование и декодирование информации |
| Биомедицина | Анализ электрокардиограмм (ЭКГ), электроэнцефалограмм (ЭЭГ), магнитно-резонансная томография (МРТ) |
| Радиолокация | Обработка радиолокационных сигналов, определение местоположения объектов |
Примеры использования БПФ в разных областях⁚
- Обработка изображений⁚ БПФ используется для сжатия изображений (например, в формате JPEG), где частотные компоненты с малой амплитудой отбрасываются, что позволяет уменьшить размер файла без значительной потери качества.
- Обработка звука⁚ В аудио редактировании БПФ позволяет анализировать спектр частот звука, что необходимо для таких операций, как шумоподавление или изменение тембра.
- Анализ временных рядов⁚ БПФ используется для анализа временных рядов в экономике, метеорологии и других областях, позволяя выявить скрытые периодичности и тренды.
Быстрое преобразование Фурье является одним из самых важных алгоритмов в современной вычислительной технике. Его эффективность и широкие возможности применения делают его незаменимым инструментом для анализа и обработки сигналов и данных. Понимание принципов работы БПФ и его различных алгоритмов позволяет разработчикам создавать новые и улучшать существующие технологии в самых разных областях.
Надеюсь, эта статья помогла вам лучше понять Быстрое преобразование Фурье. Рекомендую ознакомиться с другими нашими статьями, посвященными обработке сигналов и цифровой обработке изображений, чтобы углубить свои знания в этой области.
Хотите узнать больше о алгоритмах обработки сигналов? Прочитайте наши другие статьи, посвященные спектральному анализу и цифровой фильтрации!
Облако тегов
| Быстрое преобразование Фурье | ДПФ | Алгоритм Кули-Тьюки |
| Обработка сигналов | Обработка изображений | Обработка звука |
| Спектральный анализ | Цифровая обработка сигналов | Алгоритмы |